迭代方法

在这一部分，我们将详细讲解上个视频中提到的一些概念。

关于贝尔曼期望方程的注释

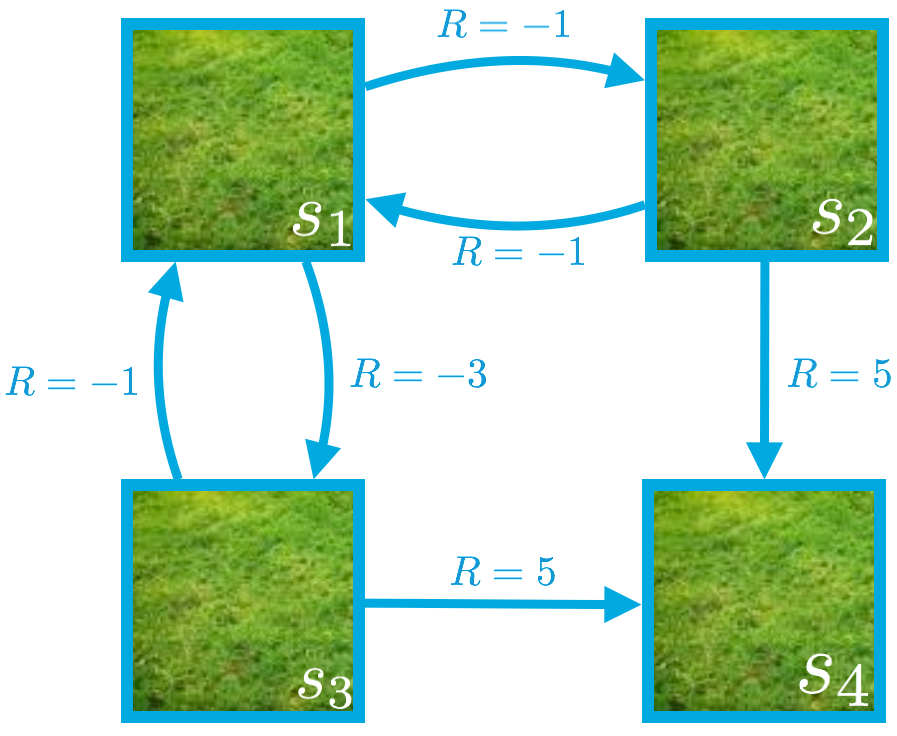
在上个视频中，我们为每个环境状态推导了一个方程。例如，对于状态 s_1，我们发现：

v_\pi(s_1) = \frac{1}{2}(-1 + v_\pi(s_2)) + \frac{1}{2}(-3 + v_\pi(s_3)).

我们提到，该方程直接来自 v_\pi 的贝尔曼期望方程。

v_\pi(s) = \text{} \mathbb{E}\pi[R{t+1} + \gamma v_\pi(S_{t+1}) | S_t=s] = \sum_{a \in \mathcal{A}(s)}\pi(a|s)\sum_{s' \in \mathcal{S}, r\in\mathcal{R}}p(s',r|s,a)(r + \gamma v_\pi(s'))（v_\pi 的贝尔曼期望方程）

为了帮助理解，我们先看看根据贝尔曼期望方程，状态 s_1 的值是多少（我们只需代入 s1 替换公式中的 s ）。

v_\pi(s_1) = \sum_{a \in \mathcal{A}(s_1)}\pi(a|s_1)\sum_{s' \in \mathcal{S}, r\in\mathcal{R}}p(s',r|s_1,a)(r + \gamma v_\pi(s'))

然后根据以下公式得出状态 s_1 的方程：

• \mathcal{A}(s_1)={ \text{down}, \text{right} }（在状态 s_1 时，智能体只能执行两个潜在动作：向下或向右。）
• \pi({down}|s_1) = \pi(\text{right}|s_1) = \frac{1}{2}（我们目前研究的策略是：智能体在状态 s_1 时向下移动的概率是 50%，向右移动的概率是 50%。）
• p(s_3,-3|s_1,\text{down}) = 1（以及 p(s',r|s_1,\text{down}) = 0，前提是 s'\neq s_3 或 r\neq -3）（如果智能体在状态 s_1 时选择向下移动，那么下个状态 100% 是 s_3，智能体获得奖励 -3。）
• p(s_2,-1|s_1,\text{right}) = 1（以及 p(s',r|s_1,\text{right}) = 0，前提是 s'\neq s_2 或 r\neq -1）（如果智能体在状态 s_1 时选择向右移动，那么下个状态 100% 是 s_2，智能体获得奖励 -1。）
• \gamma = 1（在这个网格世界示例中，我们选择将折扣率设为 1。）

如果你不太明白，请现在花时间代入值以推导出视频中的方程。然后，建议你为其他状态重复相同的流程。

关于求解方程组的注释

在视频中，我们提到你可以直接求解方程组：

v_\pi(s_1) = \frac{1}{2}(-1 + v_\pi(s_2)) + \frac{1}{2}(-3 + v_\pi(s_3))

v_\pi(s_2) = \frac{1}{2}(-1 + v_\pi(s_1)) + \frac{1}{2}(5 + v_\pi(s_4))

v_\pi(s_3) = \frac{1}{2}(-1 + v_\pi(s_1)) + \frac{1}{2}(5 + v_\pi(s_4))

v_\pi(s_4) = 0

因为 v_\pi(s_2) 和 v_\pi(s_3) 的方程一样，因此我们必须确保 v_\pi(s_2) = v_\pi(s_3)。

因此，v_\pi(s_1) 和 v_\pi(s_2) 的方程可以更改为：

v_\pi(s_1) = \frac{1}{2}(-1 + v_\pi(s_2)) + \frac{1}{2}(-3 + v_\pi(s_2)) = -2 + v_\pi(s_2)

v_\pi(s_2) = \frac{1}{2}(-1 + v_\pi(s_1)) + \frac{1}{2}(5 + 0) = 2 + \frac{1}{2}v_\pi(s_1)

将最新的两个方程相结合，生成

v_\pi(s_1) = -2 + 2 + \frac{1}{2}v_\pi(s_1) = \frac{1}{2}v_\pi(s_1)，

表明 v_\pi(s_1)=0。此外，v_\pi(s_3) = v_\pi(s_2) = 2 + \frac{1}{2}v_\pi(s_1) = 2 + 0 = 2。

因此，状态值函数可以通过以下方程组获得：

v_\pi(s_1) = 0

v_\pi(s_2) = 2

v_\pi(s_3) = 2

v_\pi(s_4) = 0

注意。此示例表明我们可以直接求解 v_\pi 的贝尔曼期望方程给出的方程组。但是，在现实中，尤其是对于大型马尔可夫决策流程 (MDP) 来说，我们将改用迭代方法。